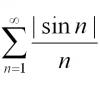Помощь
ПЕРВОЕ. Что такое графы… Это такие наборы точек (вершин графа, на рис. 1 они показаны красными кружочками) и дуг, соединяющих эти точки (эти дуги называются рёбрами графа, на том же рисунке они показаны чёрными кривыми). Граф называется уникурсальным, если его можно начертить, не отрывая кончика карандаша от бумаги и не прочерчивая никакое ребро более одного раза. Граф, изображённый на рисунке 1 – не уникурсальный. Вершина графа называется чётной, если из неё исходит чётное количество рёбер. Вершина графа называется нечётной, если из неё исходит нечётное количество рёбер. Так, на рис. 1 вершина А нечётная, потому что из неё исходит 3 ребра, а вершина В чётная, потому что из неё исходит 4 ребра.
Первый пример графа окончательный-2.JPG (84,33К)
Количество загрузок:: 8
Рис. 1
ТЕОРЕМА. Граф является уникурсальным, если у него все вершины чётные или нечётных вершин ровно 2. Если число нечётных вершин не 0 и не 2, то граф не является уникурсальным.
Поэтому-то граф, изображённый на рис. 1, и не является уникурсальным – у него 4 нечётные вершины, это вершины A, C, E, F. Поэтому же не является уникурсальным граф из задачки Гэлле.
ДАЛЬШЕ. В истории математики первой задачей на определение, является граф уникурсальным или нет, была ЗАДАЧА О КЁНИГСБЕРГСКИХ МОСТАХ, блестяще решённая великим математиком Леонардом Эйлером. Дело было так. В Кёнигсберге были 7 мостов, как они были расположены, показано на рис. 2. Здесь голубое – вода, зелёное – суша, жёлтое – мосты. И жители Кёнигсберга никак не могли решить задачу – возможно ли, и если возможно, то как произвести прогулку по местности так, чтобы пройти по каждому из мостов ровно по одному разу. Об этой задаче узнал Эйлер. Он тоже призадумался над ней, а потом решил её – доказал, что такая прогулка невозможна. Он изобразил местность с мостами в виде графа (рис. 3), сжав сушу в точки, вершины графа, и изобразив мосты рёбрами графа, а потом сформулировал и доказал теорему, приведённую выше. Задачи такого рода никогда до Эйлера не рассматривались, он был первооткрывателем.
7 мостов кёнигсберга окончательно.JPG (87,5К)
Количество загрузок:: 13
Рис. 2
граф мостов кёнигсберга окончательный.JPG (56,07К)
Количество загрузок:: 10
Рис. 3
ДОКАЗАТЕЛЬСТВО ТОГО, ЧТО ЗАДАЧА ГЭЛЛЕ ПРО РИСОВАНИЕ НЕ ОТРЫВАЯ КОНЧИКА КАРАНДАША ОТ БУМАГИ НЕ ИМЕЕТ РЕШЕНИЯ. Это доказательство даст представление о том, при чём тут вообще чётности вершин. Пусть данный граф (с рисунка Гэлле) можно нарисовать, не отрывая кончика карандаша от бумаги и не проводя рёбер более одного раза. То есть, коротко говоря, пусть данный граф уникурсальный. Рисование можно начать с какой-нибудь вершины графа. Эту вершину, с которой мы начнём, будем называть начальной. Вершину, в которой мы закончим рисовать, будем называть конечной, она может совпадать с начальной, а может не совпадать. Все вершины графа, кроме начальной и конечной, будем называть проходными. Если мы, рисуя граф, «входим» в проходную вершину, то мы обязательно должны и «выйти» из неё, ведь это вершина не конечная, мы не можем остаться в ней. На каждый «вход» по какому-либо ребру приходится «выход» по какому-либо другому ребру. Значит, из каждой проходной вершины исходит ЧЁТНОЕ количество рёбер. Значит, все проходные вершины чётные. Следовательно, нечётными вершинами могут быть максимум 2 вершины – начальная и конечная, все остальные обязательно должны быть чётными. Но в графе из задачки Гэлле нечётных вершин 4, больше двух. Мы пришли к противоречию, значит, наше предположение, что данный граф уникурсальный, неверно. Следовательно, верно, что данный граф НЕ уникурсальный, что и требовалось доказать.
ДОПОЛНЕНИЕ. Пусть мы хотим нарисовать уникурсальный граф, не отрывая кончика карандаша от бумаги. Тогда нужно учитывать следующее… Если у графа все вершины чётные, то рисовать его можно начиная с любой вершины. Заканчивать рисовать такой граф придётся в той же вершине, с которого рисовать начали. Если у графа ровно 2 вершины нечётные, то рисовать его нужно, начиная с нечётной вершины (любой из двух), а заканчивать рисование придётся тоже в нечётной вершине, но в другой, не той, с которой начали рисовать граф.
ДОПОЛНЕНИЕ 2. А ещё у любого графа число нечётных вершин чётно. В случае просьбы трудящихся я могу это доказать.
Сообщение отредактировал Решательница: 03 Март 2013 - 10:47
